前言

前期回顾：Python深度学习篇一《什么是深度学习》
上面这篇里面写了深度学习的历史及概念的介绍。

好，接下来切入正题。

要理解深度学习，需要熟悉很多简单的数学概念：张量、张量运算、微分、梯度下降等。 本章目的是用不那么技术化的文字帮你建立对这些概念的直觉。特别地，我们将避免使用数学符号，因为数学符号可能会令没有任何数学背景的人反感，而且对解释问题也不是绝对必要的。

本章将首先给出一个神经网络的示例，引出张量和梯度下降的概念，然后逐个详细介绍。 请记住，这些概念对于理解后续章节中的示例至关重要。

读完本章后，你会对神经网络的工作原理有一个直观的理解，然后就可以学习神经网络的实际应用了（从第 3 章开始）。

2.1　初识神经网络

我们来看一个具体的神经网络示例，使用Python 的 Keras 库来学习手写数字分类。如果你 没用过 Keras 或类似的库，可能无法立刻搞懂这个例子中的全部内容。甚至你可能还没有安装 Keras。没关系，下一章会详细解释这个例子中的每个步骤。因此，如果其中某些步骤看起来有 些随意，或者像魔法一样，也请你不要担心。下面我们要开始了。

我们这里要解决的问题是，将手写数字的灰度图像（28 像素×28 像素）划分到10 个类别 中（0~9）。我们将使用 MNIST 数据集，它是机器学习领域的一个经典数据集，其历史几乎和这个领域一样长，而且已被人们深入研究。这个数据集包含 60000 张训练图像和 10000 张测试图 像，由美国国家标准与技术研究院（National Institute of Standards and Technology，即 MNIST 中 的 NIST）在20 世纪80 年代收集得到。你可以将“解决”MNIST 问题看作深度学习的“Hello World”，正是用它来验证你的算法是否按预期运行。当你成为机器学习从业者后，会发现 MNIST一次又一次地出现在科学论文、博客文章等中。图2-1给出了MNIST数据集的一些样本。

关于类和标签的说明

​ 在机器学习中，分类问题中的某个类别叫作类（class）。数据点叫作样本（sample）。某 个样本对应的类叫作标签（label）。

图 2-1　MNIST 数字图像样本

你不需要现在就尝试在计算机上运行这个例子。但如果你想这么做的话，首先需要安装 Keras，安装方法见 3.3 节。

MNIST 数据集预先加载在 Keras 库中，其中包括 4 个 Numpy 数组。

代码清单 2-1　加载 Keras 中的 MNIST 数据集

from keras.datasets import mnist 
(train_images, train_labels), (test_images, test_labels) = mnist.load_data() 

train_images 和 train_labels 组成了训练集（training set），模型将从这些数据中进行学习。然后在测试集（test set，即 test_images 和 test_labels）上对模型进行测试。

图像被编码为 Numpy 数组，而标签是数字数组，取值范围为 0~9。图像和标签一一对应。

我们来看一下训练数据：

>>> train_images.shape 
(60000, 28, 28) 
>>> len(train_labels) 
60000 
>>> train_labels 
array([5, 0, 4, ..., 5, 6, 8], dtype=uint8)

下面是测试数据：

>>> test_images.shape
(10000, 28, 28) 
>>> len(test_labels) 
10000 
>>> test_labels 
array([7, 2, 1, ..., 4, 5, 6], dtype=uint8)

接下来的工作流程如下：首先，将训练数据（train_images 和 train_labels）输入神经网络；其次，网络学习将图像和标签关联在一起；最后，网络对 test_images 生成预测， 而我们将验证这些预测与 test_labels 中的标签是否匹配。

下面我们来构建网络。再说一遍，你现在不需要理解这个例子的全部内容。

代码清单 2-2　网络架构

from keras import models from keras import layers 
network = models.Sequential() network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,))) network.add(layers.Dense(10, activation='softmax')) 

神经网络的核心组件是层（layer），它是一种数据处理模块，你可以将它看成数据过滤器。 进去一些数据，出来的数据变得更加有用。具体来说，层从输入数据中提取表示——我们期望这种表示有助于解决手头的问题。大多数深度学习都是将简单的层链接起来，从而实现渐进式的数据蒸馏（data distillation）。深度学习模型就像是数据处理的筛子，包含一系列越来越精细的数据过滤器（即层）。

本例中的网络包含2 个 Dense 层，它们是密集连接（也叫全连接）的神经层。第二层（也是最后一层）是一个10 路 softmax 层，它将返回一个由10 个概率值（总和为1）组成的数组。 每个概率值表示当前数字图像属于 10 个数字类别中某一个的概率。

要想训练网络，我们还需要选择编译（compile）步骤的三个参数。

• 损失函数（loss function）：网络如何衡量在训练数据上的性能，即网络如何朝着正确的方向前进。
• 优化器（optimizer）：基于训练数据和损失函数来更新网络的机制。
• 在训练和测试过程中需要监控的指标（metric）：本例只关心精度，即正确分类的图像所 占的比例。

后续两章会详细解释损失函数和优化器的确切用途。

代码清单 2-3　编译步骤

network.compile(optimizer='rmsprop',
loss='categorical_crossentropy',
metrics=['accuracy'])

在开始训练之前，我们将对数据进行预处理，将其变换为网络要求的形状，并缩放到所有值都在[0, 1] 区间。比如，之前训练图像保存在一个uint8类型的数组中，其形状为 (60000, 28, 28)，取值区间为 [0, 255]。我们需要将其变换为一个 float32 数组，其形状为 (60000, 28 * 28)，取值范围为 0~1。

代码清单 2-4　准备图像数据

train_images = train_images.reshape((60000, 28 * 28)) 
train_images = train_images.astype('float32') / 255 

test_images = test_images.reshape((10000, 28 * 28)) 
test_images = test_images.astype('float32') / 255 

我们还需要对标签进行分类编码，第 3 章将会对这一步骤进行解释。

代码清单 2-5　准备标签

from keras.utils import to_categorical 

train_labels = to_categorical(train_labels) 
test_labels = to_categorical(test_labels) 

现在我们准备开始训练网络，在 Keras 中这一步是通过调用网络的 fit 方法来完成的—— 我们在训练数据上拟合（fit）模型。

>>> network.fit(train_images, train_labels, epochs=5, batch_size=128) 
Epoch 1/5 
60000/60000 [=============================] - 9s - loss: 0.2524 - acc: 0.9273  
Epoch 2/5 
51328/60000 [=======================>.....] - ETA: 1s - loss: 0.1035 - acc: 0.9692

训练过程中显示了两个数字：一个是网络在训练数据上的损失（loss），另一个是网络在 训练数据上的精度（acc）。

我们很快就在训练数据上达到了0.989（98.9%）的精度。现在我们来检查一下模型在测试集上的性能。

>>> test_loss, test_acc = network.evaluate(test_images, test_labels) 
>>> print('test_acc:', test_acc) 
test_acc: 0.9785 

测试集精度为97.8%，比训练集精度低不少。训练精度和测试精度之间的这种差距是过拟合（overfit）造成的。过拟合是指机器学习模型在新数据上的性能往往比在训练数据上要差，它是第 3 章的核心主题。

第一个例子到这里就结束了。你刚刚看到了如何构建和训练一个神经网络，用不到 20 行的 Python 代码对手写数字进行分类。下一章会详细介绍这个例子中的每一个步骤，并讲解其背后的原理。接下来你将要学到张量（输入网络的数据存储对象）、张量运算（层的组成要素）和梯度下降（可以让网络从训练样本中进行学习）。

2.2　神经网络的数据表示

前面例子使用的数据存储在多维Numpy 数组中，也叫张量（tensor）。一般来说，当前所有机器学习系统都使用张量作为基本数据结构。张量对这个领域非常重要，重要到Google 的 TensorFlow 都以它来命名。那么什么是张量？

张量这一概念的核心在于，它是一个数据容器。它包含的数据几乎总是数值数据，因此它是数字的容器。你可能对矩阵很熟悉，它是二维张量。张量是矩阵向任意维度的推广［注意， 张量的维度（dimension）通常叫作轴（axis）］。

2.2.1　标量（0D 张量）

仅包含一个数字的张量叫作标量（scalar，也叫标量张量、零维张量、0D 张量）。在 Numpy 中，一个 float32 或 float64 的数字就是一个标量张量（或标量数组）。你可以用 ndim 属性来查看一个 Numpy 张量的轴的个数。标量张量有 0 个轴（ndim == 0）。张量轴的个数也叫作阶（rank）。下面是一个 Numpy 标量。

>>> import numpy as np 
>>> x = np.array(12) 
>>> x array(12) 
>>> x.ndim 
0

2.2.2　向量（1D 张量）

数字组成的数组叫作向量（vector）或一维张量（1D 张量）。一维张量只有一个轴。下面是 一个 Numpy 向量。

>>> x = np.array([12, 3, 6, 14, 7]) 
>>> x array([12, 3, 6, 14, 7]) 
>>> x.ndim 
1 

这个向量有5 个元素，所以被称为 5D 向量。不要把 5D 向量和 5D 张量弄混！5D 向量只有一个轴，沿着轴有 5 个维度，而 5D 张量有5 个轴（沿着每个轴可能有任意个维度）。维度 （dimensionality）可以表示沿着某个轴上的元素个数（比如 5D 向量），也可以表示张量中轴的个 数（比如 5D 张量），这有时会令人感到混乱。对于后一种情况，技术上更准确的说法是 5 阶张量 （张量的阶数即轴的个数），但 5D 张量这种模糊的写法更常见。

2.2.3　矩阵（2D 张量）

向量组成的数组叫作矩阵（matrix）或二维张量（2D 张量）。矩阵有 2 个轴（通常叫作行和列）。你可以将矩阵直观地理解为数字组成的矩形网格。下面是一个 Numpy 矩阵。

>>> x = np.array([[5, 78, 2, 34, 0],
                    [6, 79, 3, 35, 1],
                    [7, 80, 4, 36, 2]]) 

>>> x.ndim 
2 

第一个轴上的元素叫作行（row），第二个轴上的元素叫作列（column）。在上面的例子中， [5, 78, 2, 34, 0] 是 x 的第一行，[5, 6, 7] 是第一列。

2.2.4　3D 张量与更高维张量

将多个矩阵组合成一个新的数组，可以得到一个3D 张量，你可以将其直观地理解为数字 组成的立方体。下面是一个 Numpy 的 3D 张量。

>>> x = np.array([[[5, 78, 2, 34, 0],
                        [6, 79, 3, 35, 1],
                        [7, 80, 4, 36, 2]],
                  [[5, 78, 2, 34, 0],
                      [6, 79, 3, 35, 1],
                      [7, 80, 4, 36, 2]],
                  [[5, 78, 2, 34, 0], 
                      [6, 79, 3, 35, 1], 
                      [7, 80, 4, 36, 2]]]) 

>>> x.ndim
3 

将多个 3D 张量组合成一个数组，可以创建一个 4D 张量，以此类推。深度学习处理的一般 是 0D 到 4D 的张量，但处理视频数据时可能会遇到 5D 张量。

2.2.5　关键属性

张量是由以下三个关键属性来定义的。

• 轴的个数（阶）。例如，3D 张量有3 个轴，矩阵有2 个轴。这在 Numpy 等 Python 库中 也叫张量的 ndim。
• 形状。这是一个整数元组，表示张量沿每个轴的维度大小（元素个数）。例如，前面矩阵示例的形状为 (3, 5)，3D 张量示例的形状为 (3, 3, 5)。向量的形状只包含一个元素，比如 (5,)，而标量的形状为空，即 ()。
• 数据类型（在Python 库中通常叫作 dtype）。这是张量中所包含数据的类型，例如，张量的类型可以是 float32、uint8、float64 等。在极少数情况下，你可能会遇到字符 （char）张量。注意，Numpy（以及大多数其他库）中不存在字符串张量，因为张量存储在预先分配的连续内存段中，而字符串的长度是可变的，无法用这种方式存储。

为了具体说明，我们回头看一下 MNIST 例子中处理的数据。首先加载 MNIST 数据集。

from keras.datasets import mnist 

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

接下来，我们给出张量 train_images 的轴的个数，即 ndim 属性。

>>> print(train_images.ndim) 
3

下面是它的形状

>>> print(train_images.shape) 
(60000, 28, 28)

下面是它的数据类型，即 dtype 属性。

>>> print(train_images.dtype) 
uint8 

所以，这里 train_images 是一个由 8 位整数组成的 3D 张量。更确切地说，它是60000个矩阵组成的数组，每个矩阵由 28×28 个整数组成。每个这样的矩阵都是一张灰度图像，元素取值范围为 0~255。

我们用 Matplotlib 库（Python 标准科学套件的一部分）来显示这个 3D 张量中的第 4 个数字， 如图 2-2 所示。

代码清单 2-6　显示第 4 个数字

digit = train_images[4] 

import matplotlib.pyplot as plt 
plt.imshow(digit, cmap=plt.cm.binary) 
plt.show()

图 2-2　数据集中的第 4 个样本

2.2.6　在 Numpy 中操作张量

在前面的例子中，我们使用语法 train_images[i] 来选择沿着第一个轴的特定数字。选择张量的特定元素叫作张量切片（tensor slicing）。我们来看一下 Numpy 数组上的张量切片运算。

下面这个例子选择第10~100 个数字（不包括第100 个），并将其放在形状为(90, 28, 28) 的数组中。

>>> my_slice = train_images[10:100] 
>>> print(my_slice.shape) 
(90, 28, 28)

它等同于下面这个更复杂的写法，给出了切片沿着每个张量轴的起始索引和结束索引。
注意，: 等同于选择整个轴。

>>> my_slice = train_images[10:100, :, :]   
>>> my_slice.shape 
(90, 28, 28) 
>>> my_slice = train_images[10:100, 0:28, 0:28]   
>>> my_slice.shape 
(90, 28, 28) 

一般来说，你可以沿着每个张量轴在任意两个索引之间进行选择。例如，你可以在所有图像的右下角选出 14 像素×14 像素的区域：

my_slice = train_images[:, 14:, 14:]

也可以使用负数索引。与 Python 列表中的负数索引类似，它表示与当前轴终点的相对位置。 你可以在图像中心裁剪出 14 像素×14 像素的区域：

my_slice = train_images[:, 7:-7, 7:-7]

2.2.7　数据批量的概念

通常来说，深度学习中所有数据张量的第一个轴（0 轴，因为索引从0 开始）都是样本轴 （samples axis，有时也叫样本维度）。在 MNIST 的例子中，样本就是数字图像。

此外，深度学习模型不会同时处理整个数据集，而是将数据拆分成小批量。具体来看，下面是 MNIST 数据集的一个批量，批量大小为 128。

batch = train_images[:128]

然后是下一个批量。

batch = train_images[128:256] 

然后是第 n 个批量。

batch = train_images[128 * n:128 * (n + 1)]

对于这种批量张量，第一个轴（0轴）叫作批量轴（batch axis）或批量维度（batch dimension）。 在使用 Keras 和其他深度学习库时，你会经常遇到这个术语。

2.2.8　现实世界中的数据张量

我们用几个你未来会遇到的示例来具体介绍数据张量。你需要处理的数据几乎总是以下类别之一。

• 向量数据：2D 张量，形状为 (samples, features)。
• 时间序列数据或序列数据：3D 张量，形状为 (samples, timesteps, features)。
• 图像：4D 张量，形状为 (samples, height, width, channels) 或(samples, channels, height, width)。
• 视频：5D 张量，形状为 (samples, frames, height, width, channels) 或(samples, frames, channels, height, width)。

2.2.9　向量数据

这是最常见的数据。对于这种数据集，每个数据点都被编码为一个向量，因此一个数据批量就被编码为 2D 张量（即向量组成的数组），其中第一个轴是样本轴，第二个轴是特征轴。

我们来看两个例子。

• 人口统计数据集，其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值 的向量，而整个数据集包含100 000 个人，因此可以存储在形状为 (100000, 3) 的 2D 张量中。
• 文本文档数据集，我们将每个文档表示为每个单词在其中出现的次数（字典中包含 20 000 个常见单词）。每个文档可以被编码为包含20 000 个值的向量（每个值对应于 字典中每个单词的出现次数），整个数据集包含500 个文档，因此可以存储在形状为 (500, 20000) 的张量中。

2.2.10　时间序列数据或序列数据

当时间（或序列顺序）对于数据很重要时，应该将数据存储在带有时间轴的3D 张量中。 每个样本可以被编码为一个向量序列（即2D 张量），因此一个数据批量就被编码为一个 3D 张 量（见图 2-3）。

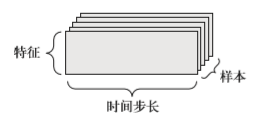
图 2-3　时间序列数据组成的 3D 张量

根据惯例，时间轴始终是第 2 个轴（索引为 1 的轴）。我们来看几个例子。

• 股票价格数据集。每一分钟，我们将股票的当前价格、前一分钟的最高价格和前一分钟的最低价格保存下来。因此每分钟被编码为一个3D 向量，整个交易日被编码为一个形 状为 (390, 3) 的 2D 张量（一个交易日有 390 分钟），而 250 天的数据则可以保存在一 个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据。
• 推文数据集。我们将每条推文编码为280 个字符组成的序列，而每个字符又来自于128 个字符组成的字母表。在这种情况下，每个字符可以被编码为大小为 128 的二进制向量 （只有在该字符对应的索引位置取值为1，其他元素都为0）。那么每条推文可以被编码 为一个形状为 (280, 128) 的 2D 张量，而包含100 万条推文的数据集则可以存储在一 个形状为 (1000000, 280, 128) 的张量中。

2.2.11　图像数据

图像通常具有三个维度：高度、宽度和颜色深度。虽然灰度图像（比如MNIST 数字图像） 只有一个颜色通道，因此可以保存在2D 张量中，但按照惯例，图像张量始终都是 3D 张量，灰度图像的彩色通道只有一维。因此，如果图像大小为256×256，那么128 张灰度图像组成的批量可以保存在一个形状为 (128, 256, 256, 1) 的张量中，而128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3）的张量中（见图2-4）。

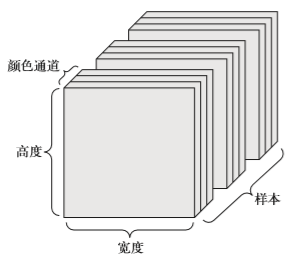
图 2-4　图像数据组成的 4D 张量（通道在前的约定）

图像张量的形状有两种约定：通道在后（channels-last）的约定（在 TensorFlow 中使用）和 通道在前（channels-first）的约定（在 Theano 中使用）。Google 的 TensorFlow 机器学习框架将颜色深度轴放在最后：(samples, height, width, color_depth)。与此相反，Theano 将图像深度轴放在批量轴之后：(samples, color_depth, height, width)。如果采用 Theano 约定，前面的两个例子将变成 (128, 1, 256, 256) 和 (128, 3, 256, 256)。 Keras 框架同时支持这两种格式。

2.2.12　视频数据

视频数据是现实生活中需要用到5D 张量的少数数据类型之一。视频可以看作一系列帧， 每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_ depth) 的 3D 张量中，因此一系列帧可以保存在一个形状为(frames, height, width, color_depth) 的 4D 张量中，而不同视频组成的批量则可以保存在一个5D 张量中，其形状为 (samples, frames, height, width, color_depth)。

举个例子，一个以每秒4 帧采样的60 秒 YouTube 视频片段，视频尺寸为144×256，这个视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3) 的张量中。总共有 106168320 个值！如果张量的数据类型（dtype）是 float32，每个值都是 32 位，那么这个张量共有 405MB。好大！你在现实生活中遇到的视频要小得多，因为它们不以 float32 格式存储，而且通常被大大压缩，比如 MPEG 格式。

2.3　神经网络的“齿轮”：张量运算

所有计算机程序最终都可以简化为二进制输入上的一些二进制运算（AND、OR、NOR 等）， 与此类似，深度神经网络学到的所有变换也都可以简化为数值数据张量上的一些张量运算（tensor operation），例如加上张量、乘以张量等。

在最开始的例子中，我们通过叠加 Dense 层来构建网络。Keras 层的实例如下所示。

keras.layers.Dense(512, activation='relu')

这个层可以理解为一个函数，输入一个 2D 张量，返回另一个 2D 张量，即输入张量的新表示。具体而言，这个函数如下所示（其中 W 是一个 2D 张量，b 是一个向量，二者都是该层的属性）。

output = relu(dot(W, input) + b)

我们将上式拆开来看。这里有三个张量运算：输入张量和张量 W 之间的点积运算（dot）、 得到的 2D 张量与向量 b 之间的加法运算（+）、最后的 relu 运算。relu(x) 是 max(x, 0)。

注意 虽然本节的内容都是关于线性代数表达式，但你却找不到任何数学符号。我发现，对于没有数学背景的程序员来说，如果用简短的 Python 代码而不是数学方程来表达数学概念， 他们将更容易掌握。所以我们自始至终将会使用 Numpy 代码。

2.3.1　逐元素运算

relu 运算和加法都是逐元素（element-wise）的运算，即该运算独立地应用于张量中的每个元素，也就是说，这些运算非常适合大规模并行实现（向量化实现，这一术语来自于 1970—1990 年间向量处理器超级计算机架构）。如果你想对逐元素运算编写简单的 Python 实现，那么可以用 for 循环。下列代码是对逐元素 relu 运算的简单实现。

def naive_relu(x):
 assert len(x.shape) == 2
 x = x.copy()
 for i in range(x.shape[0]):
 for j in range(x.shape[1]):
 x[i, j] = max(x[i, j], 0)
 return x

对于加法采用同样的实现方法。

def naive_add(x, y):
 assert len(x.shape) == 2
 assert x.shape == y.shape
 x = x.copy()
 for i in range(x.shape[0]):
 for j in range(x.shape[1]):
 x[i, j] += y[i, j]
 return x

根据同样的方法，你可以实现逐元素的乘法、减法等。

在实践中处理 Numpy 数组时，这些运算都是优化好的 Numpy 内置函数，这些函数将大量运算交给安装好的基础线性代数子程序（BLAS，basic linear algebra subprograms）实现（没装的话，应该装一个）。BLAS 是低层次的、高度并行的、高效的张量操作程序，通常用 Fortran 或 C 语言来实现。

因此，在 Numpy 中可以直接进行下列逐元素运算，速度非常快。

import numpy as np
z = x + y
z = np.maximum(z, 0.)

2.3.2　广播

上一节 naive_add 的简单实现仅支持两个形状相同的 2D 张量相加。但在前面介绍的 Dense 层中，我们将一个 2D 张量与一个向量相加。如果将两个形状不同的张量相加，会发生 什么？

如果没有歧义的话，较小的张量会被广播（broadcast），以匹配较大张量的形状。广播包含以下两步。

1. 向较小的张量添加轴（叫作广播轴），使其 ndim 与较大的张量相同。
2. 将较小的张量沿着新轴重复，使其形状与较大的张量相同。

来看一个具体的例子。假设 X 的形状是 (32, 10)，y 的形状是 (10,)。首先，我们给 y 添加空的第一个轴，这样 y 的形状变为 (1, 10)。然后，我们将 y 沿着新轴重复 32 次，这样得到的张量 Y 的形状为 (32, 10)，并且 Y[i, :] == y for i in range(0, 32)。现在， 我们可以将 X 和 Y 相加，因为它们的形状相同。

在实际的实现过程中并不会创建新的 2D 张量，因为那样做非常低效。重复的操作完全是虚拟的，它只出现在算法中，而没有发生在内存中。但想象将向量沿着新轴重复 10 次，是一种很有用的思维模型。下面是一种简单的实现。

def naive_add_matrix_and_vector(x, y):
 assert len(x.shape) == 2
 assert len(y.shape) == 1
 assert x.shape[1] == y.shape[0]
 x = x.copy()
 for i in range(x.shape[0]):
 for j in range(x.shape[1]):
 x[i, j] += y[j]
 return x

如果一个张量的形状是 (a, b, ... n, n+1, ... m)，另一个张量的形状是 (n, n+1, ... m)，那么你通常可以利用广播对它们做两个张量之间的逐元素运算。广播操作会自动应用 于从 a 到 n-1 的轴。

下面这个例子利用广播将逐元素的 maximum 运算应用于两个形状不同的张量。

import numpy as np
x = np.random.random((64, 3, 32, 10))
y = np.random.random((32, 10))
z = np.maximum(x, y)

2.3.3　张量点积

点积运算，也叫张量积（tensor product，不要与逐元素的乘积弄混），是最常见也最有用的张量运算。与逐元素的运算不同，它将输入张量的元素合并在一起。

在 Numpy、Keras、Theano 和 TensorFlow 中，都是用 * 实现逐元素乘积。TensorFlow 中的点积使用了不同的语法，但在 Numpy 和 Keras 中，都是用标准的 dot 运算符来实现点积。

import numpy as np
z = np.dot(x, y)

数学符号中的点（.）表示点积运算。

z=x.y

从数学的角度来看，点积运算做了什么？我们首先看一下两个向量 x 和 y 的点积。其计算过程如下。

def naive_vector_dot(x, y):
 assert len(x.shape) == 1
 assert len(y.shape) == 1
 assert x.shape[0] == y.shape[0]
 z = 0.
 for i in range(x.shape[0]):
 z += x[i] * y[i]
 return z

注意，两个向量之间的点积是一个标量，而且只有元素个数相同的向量之间才能做点积。

你还可以对一个矩阵 x 和一个向量 y 做点积，返回值是一个向量，其中每个元素是 y 和 x 的每一行之间的点积。其实现过程如下。

import numpy as np
def naive_matrix_vector_dot(x, y):
 assert len(x.shape) == 2
 assert len(y.shape) == 1
 assert x.shape[1] == y.shape[0]
 z = np.zeros(x.shape[0])
 for i in range(x.shape[0]):
 for j in range(x.shape[1]):
 z[i] += x[i, j] * y[j]
 return z

你还可以复用前面写过的代码，从中可以看出矩阵 - 向量点积与向量点积之间的关系。

def naive_matrix_vector_dot(x, y):
 z = np.zeros(x.shape[0])
 for i in range(x.shape[0]):
 z[i] = naive_vector_dot(x[i, :], y)
 return z

注意，如果两个张量中有一个的 ndim 大于 1，那么 dot 运算就不再是对称的，也就是说， dot(x, y) 不等于 dot(y, x)。

当然，点积可以推广到具有任意个轴的张量。最常见的应用可能就是两个矩阵之间的点积。 对于两个矩阵 x 和 y，当且仅当 x.shape[1] == y.shape[0] 时，你才可以对它们做点积 （dot(x, y)）。得到的结果是一个形状为 (x.shape[0], y.shape[1]) 的矩阵，其元素为 x 的行与 y 的列之间的点积。其简单实现如下。

def naive_matrix_dot(x, y):
 assert len(x.shape) == 2
 assert len(y.shape) == 2
 assert x.shape[1] == y.shape[0]
 z = np.zeros((x.shape[0], y.shape[1]))
 for i in range(x.shape[0]):
 for j in range(y.shape[1]):
 row_x = x[i, :]
 column_y = y[:, j]
 z[i, j] = naive_vector_dot(row_x, column_y)
 return z

为了便于理解点积的形状匹配，可以将输入张量和输出张量像图 2-5 中那样排列，利用可视化来帮助理解。

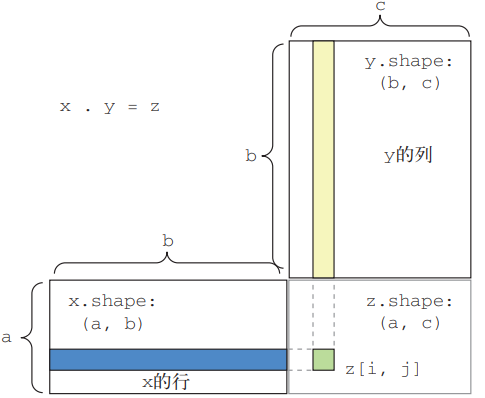
图 2-5　图解矩阵点积

图 2-5 中，x、y 和 z 都用矩形表示（元素按矩形排列）。x 的行和 y 的列必须大小相同，因此 x 的宽度一定等于 y 的高度。如果你打算开发新的机器学习算法，可能经常要画这种图。

更一般地说，你可以对更高维的张量做点积，只要其形状匹配遵循与前面 2D 张量相同的原则：

(a, b, c, d) . (d,) -> (a, b, c)
(a, b, c, d) . (d, e) -> (a, b, c, e)

以此类推。

2.3.4　张量变形

第三个重要的张量运算是张量变形（tensor reshaping）。虽然前面神经网络第一个例子的 Dense 层中没有用到它，但在将图像数据输入神经网络之前，我们在预处理时用到了这个运算。

train_images = train_images.reshape((60000, 28 * 28))

张量变形是指改变张量的行和列，以得到想要的形状。变形后的张量的元素总个数与初始张量相同。简单的例子可以帮助我们理解张量变形。

>>> x = np.array([[0., 1.],
 [2., 3.],
 [4., 5.]])
>>> print(x.shape)
(3, 2)
>>> x = x.reshape((6, 1))
>>> x
array([[ 0.],
 [ 1.],
 [ 2.],
 [ 3.],
 [ 4.],
 [ 5.]])
>>> x = x.reshape((2, 3))
>>> x
array([[ 0., 1., 2.],
 [ 3., 4., 5.]])

经常遇到的一种特殊的张量变形是转置（transposition）。对矩阵做转置是指将行和列互换， 使 x[i, :] 变为 x[:, i]。

>>> x = np.zeros((300, 20))
>>> x = np.transpose(x)
>>> print(x.shape)
(20, 300)

2.3.5　张量运算的几何解释

对于张量运算所操作的张量，其元素可以被解释为某种几何空间内点的坐标，因此所有的张量运算都有几何解释。举个例子，我们来看加法。首先有这样一个向量：

A = [0.5, 1]

它是二维空间中的一个点（见图 2-6）。

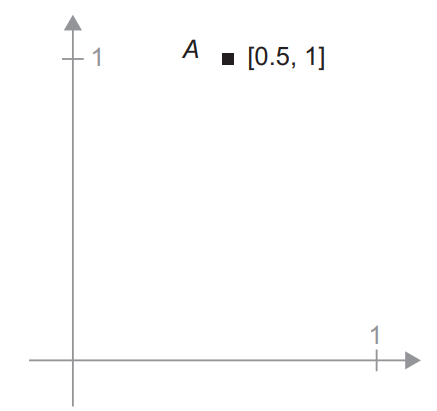
图 2-6　二维空间中的一个点

常见的做法是将向量描绘成原点到这个点的箭头， 如图 2-7 所示。

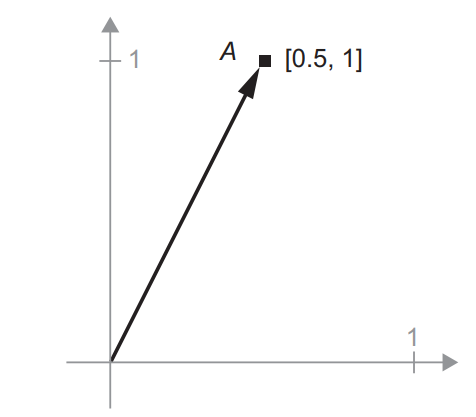
图 2-7　将二维空间中的一个点描绘成一个箭头

假设又有一个点：B = [1, 0.25]，将它与前面的 A 相加。从几何上来看，这相当于将两 个向量箭头连在一起，得到的位置表示两个向量之和对应的向量（见图 2-8）。

通常来说，仿射变换、旋转、缩放等基本的几何操作都可以表示为张量运算。举个例子，要将一个二维向量旋转 theta 角，可以通过与一个 2×2 矩阵做点积来实现，这个矩阵为 R = [u, v]，其中 u 和 v 都是平面向量：u = [cos(theta), sin(theta)]，v = [-sin(theta), cos(theta)]。

2.3.6　深度学习的几何解释

前面讲过，神经网络完全由一系列张量运算组成，而这些张量运算都只是输入数据的几何变换。因此，你可以将神经网络解释为高维空间中非常复杂的几何变换，这种变换可以通过许 多简单的步骤来实现。

对于三维的情况，下面这个思维图像是很有用的。想象有两张彩纸：一张红色，一张蓝色。

将其中一张纸放在另一张上。现在将两张纸一起揉成小球。这个皱巴巴的纸球就是你的输入数据，每张纸对应于分类问题中的一个类别。神经网络（或者任何机器学习模型）要做的就是找 到可以让纸球恢复平整的变换，从而能够再次让两个类别明确可分。通过深度学习，这一过程 可以用三维空间中一系列简单的变换来实现，比如你用手指对纸球做的变换，每次做一个动作， 如图 2-9 所示。

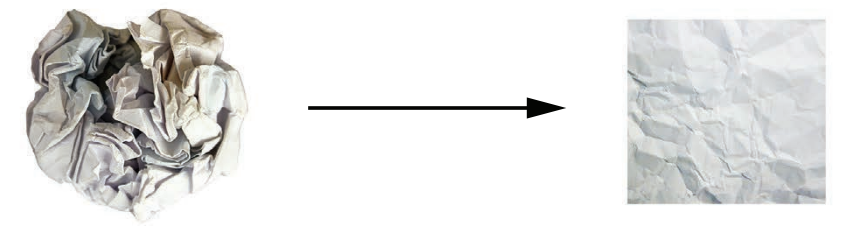
图 2-9　解开复杂的数据流形

让纸球恢复平整就是机器学习的内容：为复杂的、高度折叠的数据流形找到简洁的表示。 现在你应该能够很好地理解，为什么深度学习特别擅长这一点：它将复杂的几何变换逐步分解为一长串基本的几何变换，这与人类展开纸球所采取的策略大致相同。深度网络的每一层都通过变换使数据解开一点点——许多层堆叠在一起，可以实现非常复杂的解开过程。

2.4　神经网络的“引擎”：基于梯度的优化

上一节介绍过，我们的第一个神经网络示例中，每个神经层都用下述方法对输入数据进行 变换。

output = relu(dot(W, input) + b)

在这个表达式中，W 和 b 都是张量，均为该层的属性。它们被称为该层的权重（weight）或 可训练参数（trainable parameter），分别对应 kernel 和 bias 属性。这些权重包含网络从观察 训练数据中学到的信息。

一开始，这些权重矩阵取较小的随机值，这一步叫作随机初始化（random initialization）。 当然，W 和 b 都是随机的，relu(dot(W, input) + b) 肯定不会得到任何有用的表示。虽然得到的表示是没有意义的，但这是一个起点。下一步则是根据反馈信号逐渐调节这些权重。这个逐渐调节的过程叫作训练，也就是机器学习中的学习。

上述过程发生在一个训练循环（training loop）内，其具体过程如下。必要时一直重复这些 步骤。

1. 抽取训练样本 x 和对应目标 y 组成的数据批量。
2. 在 x 上运行网络［这一步叫作前向传播（forward pass）］，得到预测值 y_pred。
3. 计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离。
4. 更新网络的所有权重，使网络在这批数据上的损失略微下降。

最终得到的网络在训练数据上的损失非常小，即预测值 y_pred 和预期目标 y 之间的距离 非常小。网络“学会”将输入映射到正确的目标。乍一看可能像魔法一样，但如果你将其简化为基本步骤，那么会变得非常简单。

第一步看起来非常简单，只是输入 / 输出（I/O）的代码。第二步和第三步仅仅是一些张量运算的应用，所以你完全可以利用上一节学到的知识来实现这两步。难点在于第四步：更新网络的权重。考虑网络中某个权重系数，你怎么知道这个系数应该增大还是减小，以及变化多少？

一种简单的解决方案是，保持网络中其他权重不变，只考虑某个标量系数，让其尝试不同的取值。假设这个系数的初始值为 0.3。对一批数据做完前向传播后，网络在这批数据上的损失是 0.5。如果你将这个系数的值改为 0.35 并重新运行前向传播，损失会增大到 0.6。但如果你将 这个系数减小到 0.25，损失会减小到 0.4。在这个例子中，将这个系数减小 0.05 似乎有助于使损失最小化。对于网络中的所有系数都要重复这一过程。

但这种方法是非常低效的，因为对每个系数（系数很多，通常有上千个，有时甚至多达上百万个）都需要计算两次前向传播（计算代价很大）。一种更好的方法是利用网络中所有运算都是可微（differentiable）的这一事实，计算损失相对于网络系数的梯度（gradient），然后向梯度 的反方向改变系数，从而使损失降低。

如果你已经了解可微和梯度这两个概念，可以直接跳到 2.4.3 节。如果不了解，下面两小节 有助于你理解这些概念。

2.4.1　什么是导数

假设有一个连续的光滑函数 f(x) = y，将实数 x 映射为另一个实数 y。由于函数是连续的， x 的微小变化只能导致 y 的微小变化——这就是函数连续性的直观解释。假设 x 增大了一个很小的因子 epsilon_x，这导致 y 也发生了很小的变化，即 epsilon_y：

f(x + epsilon_x) = y + epsilon_y

此外，由于函数是光滑的（即函数曲线没有突变的角度），在某个点 p 附近，如果 epsilon_x 足够小，就可以将 f 近似为斜率为 a 的线性函数，这样 epsilon_y 就变成了 a * epsilon_x：

f(x + epsilon_x) = y + a * epsilon_x

显然，只有在 x 足够接近 p 时，这个线性近似才有效。

斜率 a 被称为 f 在 p 点的导数（derivative）。如果 a 是负的，说明 x 在 p 点附近的微小变化将导致 f(x) 减小（如图 2-10 所示）；如果 a 是正的，那么 x 的微小变化将导致 f(x) 增大。 此外，a 的绝对值（导数大小）表示增大或减小的速度快慢。

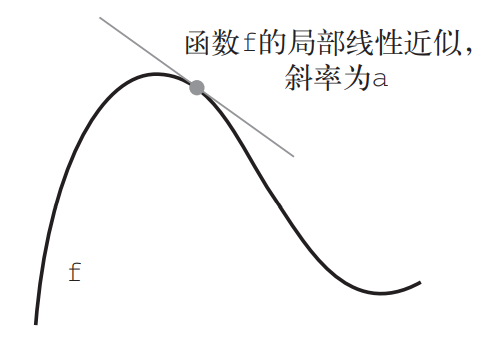
图 2-10 f 在 p 点的导数

对于每个可微函数 f(x)（可微的意思是“可以被求导”。例如，光滑的连续函数可以被求导）， 都存在一个导数函数 f'(x)，将 x 的值映射为 f 在该点的局部线性近似的斜率。例如，cos(x) 的导数是 -sin(x)，f(x) = a * x 的导数是 f'(x) = a，等等。

如果你想要将 x 改变一个小因子 epsilon_x，目的是将 f(x) 最小化，并且知道 f 的导数， 那么问题解决了：导数完全描述了改变 x 后 f(x) 会如何变化。如果你希望减小 f(x) 的值，只 需将 x 沿着导数的反方向移动一小步。

2.4.2　张量运算的导数：梯度

梯度（gradient）是张量运算的导数。它是导数这一概念向多元函数导数的推广。多元函数是以张量作为输入的函数。

假设有一个输入向量 x、一个矩阵 W、一个目标 y 和一个损失函数 loss。你可以用 W 来计算预测值 y_pred，然后计算损失，或者说预测值 y_pred 和目标 y 之间的距离。

y_pred = dot(W, x)
loss_value = loss(y_pred, y)

如果输入数据 x 和 y 保持不变，那么这可以看作将 W 映射到损失值的函数。

loss_value = f(W)

假设 W 的当前值为 W0。f 在 W0 点的导数是一个张量 gradient(f)(W0)，其形状与 W 相同， 每个系数 gradient(f)(W0)[i, j] 表示改变 W0[i, j] 时 loss_value 变化的方向和大小。 张量 gradient(f)(W0) 是函数 f(W) = loss_value 在 W0 的导数。

前面已经看到，单变量函数 f(x) 的导数可以看作函数 f 曲线的斜率。同样，gradient(f) (W0) 也可以看作表示 f(W) 在 W0 附近曲率（curvature）的张量。

对于一个函数 f(x)，你可以通过将 x 向导数的反方向移动一小步来减小 f(x) 的值。同 样，对于张量的函数 f(W)，你也可以通过将 W 向梯度的反方向移动来减小 f(W)，比如 W1 = W0 - step * gradient(f)(W0)，其中 step 是一个很小的比例因子。也就是说，沿着曲率的反方向移动，直观上来看在曲线上的位置会更低。注意，比例因子 step 是必需的，因为 gradient(f)(W0) 只是 W0 附近曲率的近似值，不能离 W0 太远。

2.4.3　随机梯度下降

给定一个可微函数，理论上可以用解析法找到它的最小值：函数的最小值是导数为 0 的点， 因此你只需找到所有导数为 0 的点，然后计算函数在其中哪个点具有最小值。

将这一方法应用于神经网络，就是用解析法求出最小损失函数对应的所有权重值。可以通过对方程 gradient(f)(W) = 0 求解 W 来实现这一方法。这是包含 N 个变量的多项式方程， 其中 N 是网络中系数的个数。N=2 或 N=3 时可以对这样的方程求解，但对于实际的神经网络是 无法求解的，因为参数的个数不会少于几千个，而且经常有上千万个。

相反，你可以使用 2.4 节开头总结的四步算法：基于当前在随机数据批量上的损失，一点一点地对参数进行调节。由于处理的是一个可微函数，你可以计算出它的梯度，从而有效地实 现第四步。沿着梯度的反方向更新权重，损失每次都会变小一点。

1. 抽取训练样本 x 和对应目标 y 组成的数据批量。
2. 在 x 上运行网络，得到预测值 y_pred。
3. 计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离。
4. 计算损失相对于网络参数的梯度［一次反向传播（backward pass）］。
5. 将参数沿着梯度的反方向移动一点，比如 W -= step * gradient，从而使这批数据上的损失减小一点。

这很简单！我刚刚描述的方法叫作小批量随机梯度下降（mini-batch stochastic gradient descent， 又称为小批量 SGD）。术语随机（stochastic）是指每批数据都是随机抽取的（stochastic 是 random 在科学上的同义词 a）。图 2-11 给出了一维的情况，网络只有一个参数，并且只有一个训练样本。

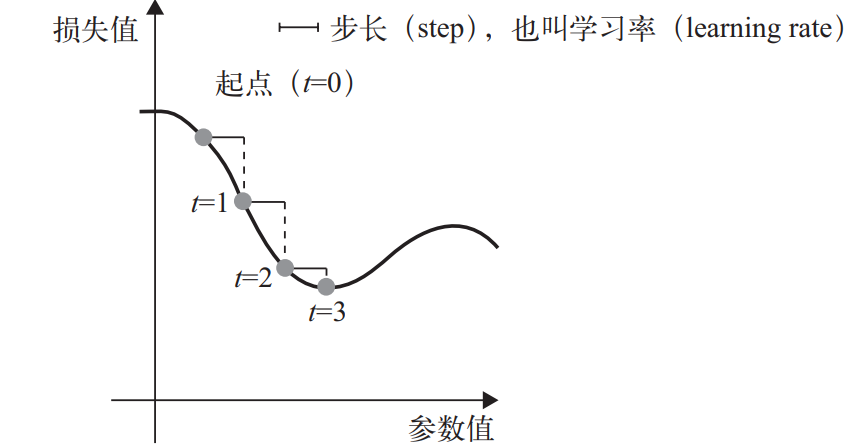
图 2-11　沿着一维损失函数曲线的随机梯度下降（一个需要学习的参数）

如你所见，直观上来看，为 step 因子选取合适的值是很重要的。如果取值太小，则沿着曲线的下降需要很多次迭代，而且可能会陷入局部极小点。如果取值太大，则更新权重值之后 可能会出现在曲线上完全随机的位置。

注意，小批量 SGD 算法的一个变体是每次迭代时只抽取一个样本和目标，而不是抽取一批数据。这叫作真 SGD（有别于小批量 SGD）。还有另一种极端，每一次迭代都在所有数据上运行，这叫作批量 SGD。这样做的话，每次更新都更加准确，但计算代价也高得多。这两个极端之间的有效折中则是选择合理的批量大小。

图 2-11 描述的是一维参数空间中的梯度下降，但在实践中需要在高维空间中使用梯度下降。 神经网络的每一个权重参数都是空间中的一个自由维度，网络中可能包含数万个甚至上百万个参数维度。为了让你对损失曲面有更直观的认识，你还可以将梯度下降沿着二维损失曲面可视化， 如图 2-12 所示。但你不可能将神经网络的实际训练过程可视化，因为你无法用人类可以理解的方式来可视化 1000000 维空间。因此最好记住，在这些低维表示中形成的直觉在实践中不一定 总是准确的。这在历史上一直是深度学习研究的问题来源。

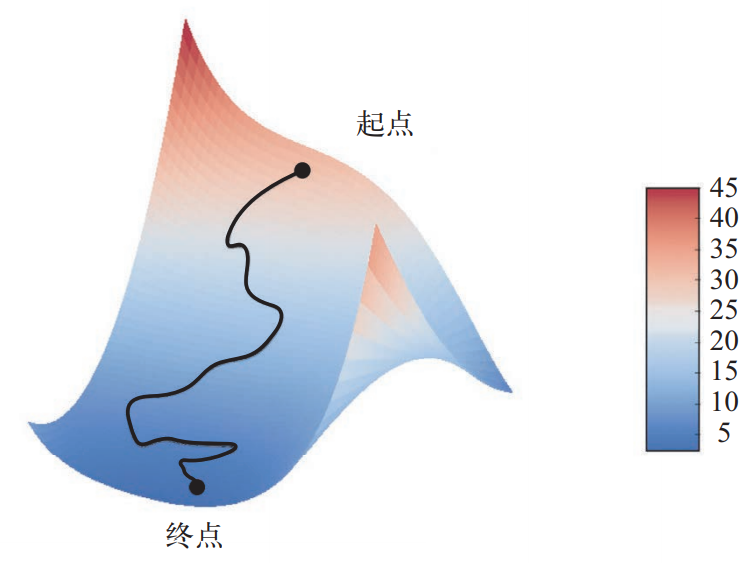
图 2-12　沿着二维损失曲面的梯度下降（两个需要学习的参数）

此外，SGD 还有多种变体，其区别在于计算下一次权重更新时还要考虑上一次权重更新， 而不是仅仅考虑当前梯度值，比如带动量的 SGD、Adagrad、RMSProp 等变体。这些变体被称为优化方法（optimization method）或优化器（optimizer）。其中动量的概念尤其值得关注，它在许多变体中都有应用。动量解决了 SGD 的两个问题：收敛速度和局部极小点。图 2-13 给出了 损失作为网络参数的函数的曲线。

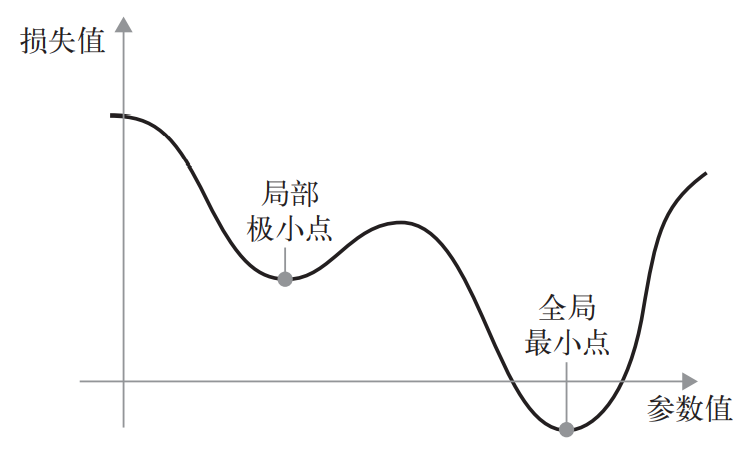
图 2-13　局部极小点和全局最小点

如你所见，在某个参数值附近，有一个局部极小点（local minimum）：在这个点附近，向 左移动和向右移动都会导致损失值增大。如果使用小学习率的 SGD 进行优化，那么优化过程可 能会陷入局部极小点，导致无法找到全局最小点。

使用动量方法可以避免这样的问题，这一方法的灵感来源于物理学。有一种有用的思维图像， 就是将优化过程想象成一个小球从损失函数曲线上滚下来。如果小球的动量足够大，那么它不会 卡在峡谷里，最终会到达全局最小点。动量方法的实现过程是每一步都移动小球，不仅要考虑当 前的斜率值（当前的加速度），还要考虑当前的速度（来自于之前的加速度）。这在实践中的是指， 更新参数 w 不仅要考虑当前的梯度值，还要考虑上一次的参数更新，其简单实现如下所示。

past_velocity = 0.
momentum = 0.1
while loss > 0.01:
 w, loss, gradient = get_current_parameters()
 velocity = past_velocity * momentum - learning_rate * gradient
 w = w + momentum * velocity - learning_rate * gradient
 past_velocity = velocity
 update_parameter(w)

2.4.4　链式求导：反向传播算法

在前面的算法中，我们假设函数是可微的，因此可以明确计算其导数。在实践中，神经网 络函数包含许多连接在一起的张量运算，每个运算都有简单的、已知的导数。例如，下面这个 网络 f 包含 3 个张量运算 a、b 和 c，还有 3 个权重矩阵 W1、W2 和 W3。

f(W1, W2, W3) = a(W1, b(W2, c(W3)))

根据微积分的知识，这种函数链可以利用下面这个恒等式进行求导，它称为链式法则（chain rule）：(f(g(x)))' = f'(g(x)) * g'(x)。将链式法则应用于神经网络梯度值的计算，得到的算法叫作反向传播（backpropagation，有时也叫反式微分，reverse-mode differentiation）。反 向传播从最终损失值开始，从最顶层反向作用至最底层，利用链式法则计算每个参数对损失值 的贡献大小。

现在以及未来数年，人们将使用能够进行符号微分（symbolic differentiation）的现代框架来实现神经网络，比如 TensorFlow。也就是说，给定一个运算链，并且已知每个运算的导数，这些框架就可以利用链式法则来计算这个运算链的梯度函数，将网络参数值映射为梯度值。对于这样的函数，反向传播就简化为调用这个梯度函数。由于符号微分的出现，你无须手动实现反向传播算法。因此，我们不会在本节浪费你的时间和精力来推导反向传播的具体公式。你只需 充分理解基于梯度的优化方法的工作原理。

2.5　回顾第一个例子

你已经读到了本章最后一节，现在应该对神经网络背后的原理有了大致的了解。我们回头 看一下第一个例子，并根据前面三节学到的内容来重新阅读这个例子中的每一段代码。

下面是输入数据。

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 28 * 28))
test_images = test_images.astype('float32') / 255

现在你明白了，输入图像保存在 float32 格式的 Numpy 张量中，形状分别为 (60000, 784)（训练数据）和 (10000, 784)（测试数据）。

下面是构建网络。

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28 * 28,)))
network.add(layers.Dense(10, activation='softmax'))

现在你明白了，这个网络包含两个 Dense 层，每层都对输入数据进行一些简单的张量运算， 这些运算都包含权重张量。权重张量是该层的属性，里面保存了网络所学到的知识（knowledge）。

下面是网络的编译。

network.compile(optimizer='rmsprop',
 loss='categorical_crossentropy',
 metrics=['accuracy'])

现在你明白了，categorical_crossentropy 是损失函数，是用于学习权重张量的反馈信号，在训练阶段应使它最小化。你还知道，减小损失是通过小批量随机梯度下降来实现的。 梯度下降的具体方法由第一个参数给定，即 rmsprop 优化器。

最后，下面是训练循环。

network.fit(train_images, train_labels, epochs=5, batch_size=128)

现在你明白在调用 fit 时发生了什么：网络开始在训练数据上进行迭代（每个小批量包含 128 个样本），共迭代 5 次［在所有训练数据上迭代一次叫作一个轮次（epoch）］。在每次迭代过程中，网络会计算批量损失相对于权重的梯度，并相应地更新权重。5 轮之后，网络进行了 2345 次梯度更新（每轮 469 次），网络损失值将变得足够小，使得网络能够以很高的精度对手写数字进行分类。

到目前为止，你已经了解了神经网络的大部分知识。

转载请注明：虚坏叔叔 » Python深度学习篇二《神经网络的数学基础》